ICLR 2023 Oral | 漂移感知动态神经网络加持，时间域泛化新框架远超领域泛化&适应方法

• 作者：Guangji Bai*、Chen Ling*、Liang Zhao (* equal contribution)
  
• 单位：Emory University
  
• 论文链接：https://arxiv.org/abs/2205.10664
  

情景导入

领域泛化是近几年非常热门的研究方向，它研究的问题是从若干个具有不同数据分布的数据集 (领域) 中学习一个泛化能力强的模型，以便在未知 (Unseen) 的测试集上取得较好的效果。目前。大部分领域泛化的工作假设领域之间的边界 (boundary) 是明确的且模型泛化是离线的 (offline)。然而在现实世界中，领域之间的

边界

往往是未知且难以获取的，同时领域的分布是

渐变

的，从而领域之间存在

概念漂移

(concept drift) 。

例如，当一家银行利用模型来预测一个人是否会成为「违约借款人」时，会考虑「年收入」、「职业类型」和「婚姻状况」等特征。由于社会随着时间不断演化，这些特征对于最终预测的影响也会相应地随时间而变化。

如图 1 所示，另一个例子是通过每年的推特 (Twitter) 数据来预测比如流感的爆发。推特数据每年都会不断发生变化，例如用户数量逐年上升，新的好友关系不断增加，主流用户的年龄分布不断变化等等，而这种数据分布随时间的不断变化将使得模型逐渐过时。相应地，假设有一个理想的、始终保持最新的模型，那么模型

参数

应该相应地逐渐变化以对抗数据分布随时间变化的趋势，它还可以「预测」模型

参数

在任意 (不太远) 的未来时间点应该是什么样子。因此，我们需要时间域泛化的技术来解决上述问题。

图 1：时间域泛化的说明性示例

存在的挑战

将领域索引 (domain index) 视为分类变量 (categorical variable) 的现有领域泛化方法一般不适用于时间域泛化问题，因为它们需要领域边界作为先验来学习从源域到目标域的

映射

。扩展现有的领域泛化方法来解决时间域泛化面临着以下挑战：

• 
  难以刻画数据分布的漂移及其对预测模型的影响
  
  。对随时间变化的分布建模需要使模型对时间敏感 (time-sensitive) 。现有方法无论是直接将时间作为输入数据的特征，或是将模型
  
  参数
  
  仅仅视作随时间变化的函数，只要模型的动态和数据的动态没有被整体建模，这些方法就不能很好地将模型泛化到未来的数据。
  
• 
  在追踪模型动态时缺乏表达能力
  
  。如今，
  
  深度学习
  
  的成功离不开大模型 (例如 Transformer)，其中
  
  神经元
  
  和模型
  
  参数
  
  连接成为一个复杂的计算图，然而这也极大增加了时间域泛化问题中追踪模型动态的难度。一个具有强表达能力的模型动态刻画及预测需要将数据动态
  
  映射
  
  到模型动态，也就是模型
  
  参数
  
  诱导的计算图随时间变化的动态。
  
• 
  难以对模型性能给出理论上的保障
  
  。虽然在
  
  独立同分布
  
  的假设下对
  
  机器学习
  
  问题有着丰富的理论分析，但类似理论难以推广到分布外 (Out-of-Distribution, OOD) 假设以及数据分布随时间变化的时间域泛化问题。因此，有必要加强关于不同时间域泛化模型的能力及关系的理论分析。
  

解决思路及贡献

基于上述挑战，我们提出了一种

具有漂移

感知

的动态

神经网络

的时间域泛化框架 DRAIN (Drift-A ware DynamIc Neural Networks)

。

具体而言，我们提出了一个基于

贝叶斯理论

的通用框架，通过联合建模数据和模型动态之间的关系来处理时间域泛化问题。为了实现贝叶斯框架，利用了带有循环结构的

图生成

场景来编码和解码跨不同时间点 (timestamp) 的动态图结构 (dynamic graph-structured)

神经网络

。上述场景可以实现完全时间敏感 (fully time-sensitive) 的模型，同时允许端到端 (end2end) 的训练方式。该方法能够捕获模型

参数

和数据分布随时间的漂移，并且可以在

没有

未来数据的情况下预测未来的模型。

该研究的

主要贡献

可以概括为以下几点：

• 开发了一种全新的基于
  
  贝叶斯理论
  
  的自适应时间域泛化框架，可以按照端到端的方式进行训练。
  
• 创造性地将
  
  神经网络
  
  模型视为动态图，并利用
  
  图生成
  
  技术来实现完全时间敏感的模型。
  
• 提出使用序贯 (sequential) 模型自适应地学习时间漂移，并利用学习到的序贯模型来预测未来时域的模型状态。
  
• 我们对所提出方法在未来时域上的不确定性
  
  量化
  
  (uncertainty quantification) 以及泛化误差 (generalization error) 进行了理论分析。
  
• DRAIN 框架在多个公开真实世界数据集上显著超过了以往的领域泛化和领域适应方法，在时间域泛化任务上取得 SOTA。
  

问题描述

我们给出正式的时间域泛化 (temporal DG) 的问题定义。

首先，我们考虑的是当数据分布随时间变化的情景。训练时，给定任意 T 个时间点 t_1≤t_2≤⋯≤t_T，我们有每个时间点观测到的源领域 D_1,D_2,⋯,D_T, 其中

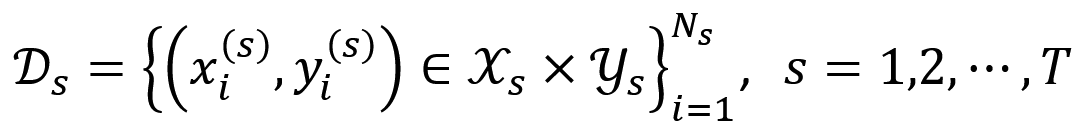
。这里，x_i^((s) )、y_i^((s) )、N_s 分别对应时间点 t_s 的样本输入特征、标签以及样本量，X_s、Y_s 表示时间点 t_s 的特征及标签空间。训练好的模型将在

未知

的未来时刻 t_(T+1)>t_T 的领域 D_(T+1) 上进行测试。由于是领域泛化问题，因此训练过程中不允许出现任何未来领域 D_(T+1) 的信息，例如无标签数据。

时间域泛化进一步假设存在时间维度的概念漂移，即领域 D_1,D_2,⋯,D_T 的分布遵循某种时间维度的模式而变化。例如，如果我们考虑个人收入每年如何变化，我们会发现由于通货膨胀，平均收入通常每年以某种比率增加。房价、教育成本等随时间的变化也存在类似规律。

我们的

目标

是建立一个能够主动且自适应地捕捉概念漂移的模型。给定源领域 D_1,D_2,⋯,D_T，我们希望对每一个领域 D_s 学习一个

映射

g_(ω_s ):X_s→Y_s，s=1,2,⋯,T。这里 ω_s 表示时刻 t_s 时的模型

参数

。最终，我们预测未来某未知领域 D_(T+1) 上的

映射

g_(ω_(T+1) ):X_(T+1)→Y_(T+1) 对应的模型

参数

ω_(T+1)。如上图 1 所示，由于数据分布的时间漂移 (例如推特用户的年龄分布和推文数量逐年增加)，预测模型应当随之演变 (例如模型

参数


权重

的大小逐年递减)。

技术方案

这里介绍我们如何解决上述三个挑战。

对于挑战 1，我们通过构建一个系统的贝叶斯概率框架来显式地 (explicitly) 描述领域间随时间的概念漂移，这也是该工作与现有 DG 方法的本质区别。

对于挑战 2，我们提出将具有随时间变化

参数

的

神经网络

建模为动态图，并实现可以通过

图生成

技术进行端到端训练的时间域泛化框架；我们通过在不同域上引入残差连接 (skip connection) 模块进一步提高所提出方法的泛化能力以及对遗忘的鲁棒性。

最后，对于挑战 3，我们探索了在具有挑战性的时间域泛化设定下模型性能的理论保证，并提供了所提出方法的理论分析，例如不确定性

量化

和泛化误差。

1. 时间漂移的概率学描述

想要在随时间变化的领域上进行领域泛化，我们需要获得给定时间间隔内的概念漂移。从概率学的角度来看，对每一个源领域 D_s，s=1,2,⋯,T， 我们通过最大化条件概率 Pr⁡(ω_s│D_s ) 训练得到

神经网络

g_(ω_s )。由于 D_s 概率随时间的演化，Pr⁡(ω_s│D_s ) 也会不断随时间改变。我们的终极目标是基于所有源领域 D_1,D_2,⋯,D_T 来预测未来某未知领域上的模型

参数

ω_(T+1)，即 Pr⁡(ω_(T+1)│D_(1:T) )。通过全概率公式 (Law of Total Probability)，我们知道

这里 Ω 表示所有

参数

ω_(1:T) 所在的空间。积分号里的第一项代表推理阶段 (inference phase)，即如何通过所有源领域上的历史信息来推断未来时刻的模型

参数

；第二项代表训练阶段，即如何通过每一个源领域的数据来得到对应的每个时间点上的模型信息。进一步，通过概率

链式法则

(chain rule of probability)，上式当中的训练阶段可以被分解为

图 2：DRAIN 总体框架示意图。

这里，我们假设在任意时间点 t_s，模型

参数

ω_s 只和当前领域以及历史领域有关，即 \{D_i:i≤s\}，同时，没有任何关于未来领域的信息。通过上式，复杂的训练过程被分解为 T-1 步，而每一步对应于如何利用当前领域数据及模型历史信息来学习当前时刻的模型

参数

，即

2. 神经网路的动态图表示

由于数据分布随时间的变化，模型

参数

也需要不断更新来适应时间漂移。我们考虑通过动态图来建模

神经网络

，以求达到最大化表达能力。

直观上讲，一个

神经网络

g_ω 可以被表示为一个

边加权图

G=(V,E,ψ)，其中节点 v∈V 表示

神经网络

中的

神经元

，而边 e∈E 则对应不同

神经元

中的连接。函数 ψ:E→R 表示边的

权重

，即

神经网络

的

参数

值。注意，这里关于边加权图的定义是非常广义 (general) 的，涵盖了浅层模型 (即 linear model) 以及常见的深度模型 (MLP、CNN、RNN、GNN) 。我们通过优化边加权图中边的

权重

来学习得到

神经网络


参数

随时间漂移的变化。

该工作中，我们考虑

神经网络

的结构是已知且固定的，即 V,E 不变，而边的

权重

随时间变化。由此，可以得到 ω_s=ψ(E│s)，其中 ψ(⋅│s) 只依赖时间 t_s。这样，三元组 G=(V,E,ψ_s ) 定义了一个带有动态边

权重

的

时间图

(temporal graph) 。

3. 时间漂移的端到端学习

给定

神经网络

在历史领域

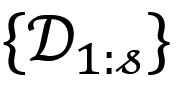
上学习得到的历史状态 \{ω_(1:s) \}，我们的目标是如何端到端地外插得到

神经网络

在新的领域

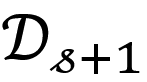
上的

参数

状态 ω_(s+1)，并且得到良好的预测性能。事实上，考虑到我们将

神经网络

的

参数

变化 {ω_(1:s)} 视作一个动态网络的演化，一个自然的方法即为通过模拟 {ω_(1:s)} 随时间如何演化来学习得到该动态网络的隐分布 (latent distribution)。最终，我们从动态网络的隐分布中采样即可得到未来时间点

神经网络


参数

的预测值 ω_(s+1)。

我们将学习 {ω_(1:s)} 的隐分布刻画为一个基于循环结构的顺序学习过程。如上图 2 所示，在任意训练时刻 t_s，递归网络会基于历史信息 {ω_i:i<s} 来生成 ω_s。具体而言，我们考虑 LSTM 作为递归网络的实现，并用 f_θ 来表示 LSTM unit，那么 f_θ 在 t_s 时刻有两个输出：当前的记忆状态 (memory state) m_s，以及包含了历史信息的隐

概率分布

h_s，而隐

概率分布

h_s 使得我们能够利用一个图解码器 F_ξ (⋅) 来生成得到动态网络当前时刻的

参数

状态 ω_s。

不同于现有的在单个域上训练和

正则化


神经网络

的工作，在这里我们专注于直接搜索具有「良好结构」的网络分布。最后，采样得到的当前时刻

神经网络


参数

ω_s 被图编码器 G_η (⋅) 转化为 f_θ 在下一时刻的输入。整个框架顺序地在每一个训练领域上优化，即基于当前领域训练集

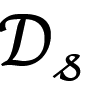
来生成 ω_s 来最小化以下

目标函数

这里

损失函数


由具体任务决定，比如回归任务的 MSE 或者分类任务的 cross-entropy。

4. 更少的遗忘和更好的泛化能力

在训练递归

神经网络

时，可能会遇到性能下降的问题。由于领域之间存在时间维度上复杂的相关性，该问题在时间域泛化中可能会更严重。而且，当源领域的数量很大的时候，我们发现还可能出现灾难性遗忘 (catastrophic forgetting) 的问题。为了减轻该问题对模型性能的影响，我们提出了通过残差连接技术来增强不同领域训练模型时的相关性。具体而言，

其中 λ 为超参，s 为滑动窗口 (sliding window) 的宽度。残差连接的使用能够使得新生成的模型

参数

ω_s 包含部分历史领域的信息，而定长的滑动窗口能够保证至多线性的算法复杂度。

理论分析

我们从理论角度探讨了所提出框架 DRAIN 在时间域泛化问题上的优越性：(1) 更小的预测不确定性；(2) 更小的泛化误差。首先给出一些必要的定义以及假设：

接下来的定理 1 表明，通过学习潜在的时维度的概念漂移，DRAIN 能够在测试领域上取得更小的预测方差，即更小的不确定性：

下面的定理 2 表明，除了预测的方差，我们的方法 DRAIN 同样可以在测试领域上取得更小的泛化误差，即更高的泛化精度：

实验结果

为了验证算法效果，我们在 7 个带有时间漂移的数据集 (5 个分类、2 个回归) 上进行试验，并与多个 DA 和 DG 方法进行比较。实验结果可见下表 1，其中我们提出的框架 DRAIN 在几乎所有数据集均取得了最优的泛化性能。相较于 CDOT/CIDA/GI 等方法，DRAIN 通过递归网络从本质上解决概念漂移问题，从而能够以更强的表达能力来端到端地学习时间漂移。

进一步，我们在 2-Moons 数据集上对各个方法的

决策边界

(decision boundary) 进行了可视化实验，从而更清晰地展现出 DRAIN 的性能提升。通过横向比较下图 3 (d) 和图 4 (a)-(f) 的右子图 (均为测试领域上的

决策边界

)，我们发现 DRAIN 框架在未来领域上拥有最准确的

决策边界

，再一次验证所提出方法对概念漂移的捕捉能力以及时间维度的泛化能力。

对于所提出框架 DARIN，动态

神经网络

的层深是一个重要的

参数

，它控制着性能与计算成本的权衡。我们探索了所提出框架 DRAIN 性能对于所生成

神经网络

层深的

敏感性分析

，由下图 5 可见在 2-Moons 以及 Elec2 数据集曲线均呈现出倒 U 型。过浅的网络会缺乏表达能力，而过深的网络则会减弱泛化能力。

最后，我们同样进行了消融实验 (ablation study)，来进一步探究不同模块 (module) 对于所提出框架 DRAIN 的贡献和影响。如下表 2 所示，每个模块都可以有效地促进整体框架的性能，通过递归模型对所有时间域的相关性进行建模可以提供相当大的性能增益。此外，删除顺序学习模型中的跳跃连接会使 DRAIN 难以捕获域之间的远程时间依赖性，因为在模型学习期间可能会忘记遥远的历史领域信息。

结论

我们通过提出基于动态

神经网络

的框架来解决时间域泛化问题，构建了一个贝叶斯框架来对概念漂移进行建模，并将

神经网络

视为一个动态图来捕捉随时间不断变化的趋势。我们提供了所提出框架的理论分析（例如预测的不确定性和泛化误差）以及广泛的实证结果，从而证明我们的方法与最先进的 DA 和 DG 方法相比的有效性和效率。